حاسبة الجبر المنطقية هي تيار الرياضيات الذي يتكون من التعبيرات المنطقية والمتغيرات المنطقية التي تعالج. ينفذ العمليات المنطقية مثل AND و NAND و OR و NOR و NOT & X-OR . يتم الإشارة إلى قيم آلة حاسبة الجبر المنطقي بالمنطق 0 & 1. تستخدم حاسبة الجبر المنطقية القوانين الأساسية مثل قانون الهوية والقانون التبادلي وقانون التوزيع والقانون المنتسب وقانون التكرار. الغرض الرئيسي من هذا القانون يستخدم لإنجاز العمليات المنطقية مثل المساواة ، والفصل ، والاقتران ، والتضمين. يمكن التعبير عن العمليات المنطقية بطرق مختلفة ، مثل: تم ذكر الاقتران (a ^ b) على أنه a و b ، يُذكر الفصل (a V b) على أنه a أو b ، والتضمين (a b) مذكور ضمنيًا يُشار ب & المساواة (أب) إلى ص س ولا ف.

حاسبة الجبر المنطقية
يشبه تطبيق الجبر المنطقي حالة التبديل الكهربائي التي يمكن أن تكون إما قيم منطقية 0 و 1. تعطي حاسبة الجبر المنطقية النتيجة على الفور في شكل تعبير رياضي عن طريق تنفيذ عمليات مثل الجمع والضرب وما إلى ذلك. آلة حاسبة سهلة للغاية وسهلة الاستخدام
منطقية الجبر حاسبة كتلة الرسم التخطيطي
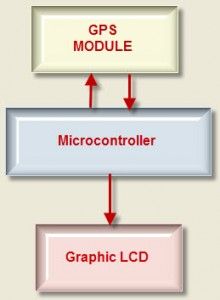
يتضمن مخطط كتلة آلة حاسبة الجبر المنطقية كتل مختلفة مثل مزود الطاقة ولوحة المفاتيح والميكروكونترولر و عرض الصمام .

منطقية الجبر حاسبة كتلة الرسم التخطيطي
يستخدم مصدر الطاقة لإعطاء الطاقة لدائرة البومة ، ويقوم بتحويل أشكال مختلفة من الطاقات مثل الطاقة الشمسية والميكانيكية والكيميائية إلى طاقة كهربائية. يستخدم هذا المشروع 5V من الطاقة والتي يتم إعطاؤها للوحة المفاتيح والشاشة والميكروكونترولر. يتم استخدام متحكم دقيق لقراءة البيانات من لوحة المفاتيح وإرسال البيانات إلى ملف عرض شاشات الكريستال السائل . يلعب الميكروكونترولر دورًا حيويًا في هذا المشروع والذي تمت برمجته بواسطة a برنامج الوتد .
في هذا المشروع ، يتم استخدام شاشة LED ثلاثية الألوان لعرض النمط المتوهج للتعبير. تشير هذه الألوان الثنائية إلى الوضع الطبيعي والمكمل للمتغيرات مثل المفاتيح. تُستخدم لوحة المفاتيح في هذا المشروع لإعطاء المصطلحات min مثل i / p أي ، كل رقم على لوحة المفاتيح يستجيب لكل مصطلح min.
حلبة حاسبة الجبر المنطقية
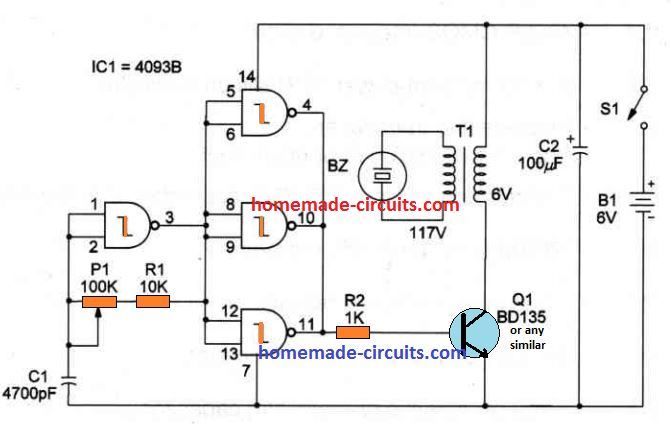
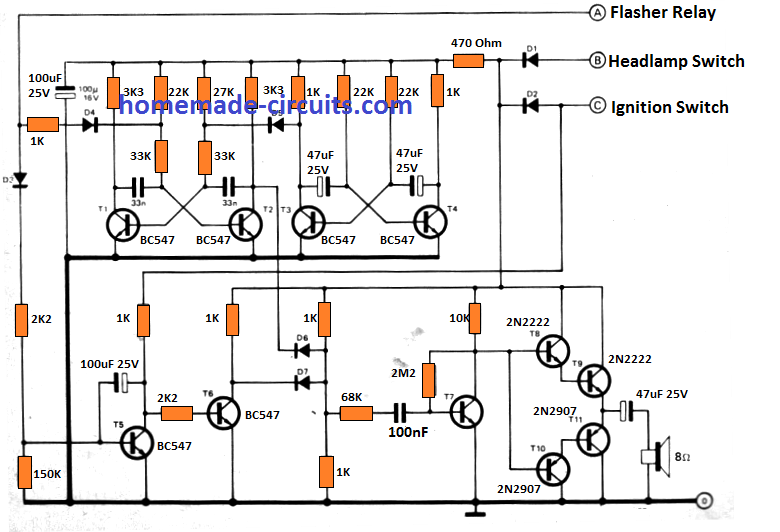
يعد الرسم التخطيطي لدائرة حاسبة الجبر المنطقي التالي منخفض التكلفة وسريع الأداء منخفض الطاقة وموثوقًا. هذه الدائرة مبنية بشكل بسيط المكونات الكهربائية والإلكترونية المتوفرة في السوق مثل المقاومات ولوحة المفاتيح وشاشة LCD والميكروكونترولر كما هو موضح في الدائرة التالية.

حلبة حاسبة الجبر المنطقية
تتكون الدائرة المذكورة أعلاه من ثلاثة مُصغرات متغيرة ، تستخدم 'خوارزمية Quine MC Cluskey' وتجد الحد الأدنى من المنتجات عن طريق تنفيذ وظائف Boolean. هذه الآلة الحاسبة تحل التعبيرات المنطقية و وظائف المنطق باستخدام نظريات وقوانين مختلفة. يلعب المتحكم الدقيق المستخدم في هذا المشروع دورًا حيويًا ، يتم ترميزه ببرنامج ويتحكم في المكونات المستخدمة في هذه الدائرة.
عندما يتم توفير مصدر الطاقة للدائرة ، يومض مؤشر LED. يشير وميض LED إلى أن وحدة التحكم الدقيقة جاهزة لاستقبال i / ps من لوحة المفاتيح. يتم إعطاء هذه التعبيرات المنطقية في شكل مجموع المنتجات (SOP).
يستخدم هذا المشروع لوحة مفاتيح ، تتكون من 9 مفاتيح ، حيث يتم استخدام ثمانية مفاتيح تتعلق بمصطلحات الحد الأدنى التي تنفذ عملية المنتج ويتم استخدام المفتاح المتبقي كزر تالي. عندما يتم إدخال التعبير ، يتم إيقاف تشغيل مؤشر LED ، وبناءً على الخوارزمية ، يقوم الميكروكونترولر بتقليل تعبير المصطلح الأدنى. ثم يومض مؤشر i / p LED مما يعني أنه تم تصغير التعبير وعرضه على مؤشر LED.
يظهر o / p كمصطلح min مرة واحدة ، ويظهر المصطلح min الثاني بالضغط على الزر التالي. لذلك ، بعد الحصول على المصطلح الأخير ، سيتم تقليل التعبير ويتم إيقاف تشغيل i / p LED الذي يوضح أن o / p قد انتهى ، ثم تلقائيًا ، يتم تشغيل LED للإشارة إلى أن المتحكم الدقيق جاهز لاتخاذ المزيد ص.
تبسيط التعبير المنطقي
العبارات التالية هي مثال على التعبيرات المنطقية باستخدام تقنيات جبرية.
التعبير هو ~ (A * B) * (~ A + B) * (~ B + B) = ~ A
- ~ (أ * ب) * (~ أ + ب) * (~ ب + ب)
- قانون الهوية والقانون المكمل هو ~ (أ * ب) * (~ أ + ب).
- القانون وDeMorgan ل(~ A ~ + B) * (~ A + B)
- قانون التوزيع هو ~ A + ~ B * B
- ~ A مجاملة أو هوية.
كل خطوة تعطي صيغة معادلة ويتم استخدام القواعد لحل المعادلات من المعادلات السابقة. بشكل عام ، هناك طرق مختلفة للوصول إلى النتيجة.
قوانين الجبر المنطقية
هناك العديد من القوانين لحلها التعبيرات المنطقية. نظريات الجبر البولي هي على وجه التحديد Idempotent Associative و Commutative و Distribution و Identity و Complement و Involution و DeMorgan’s.
قانون العدم
أ * أ = أ
أ + أ = أ
القانون الترابطي
(أ * ب) * ج = أ * (ب * ج)
(أ + ب) + ج = أ + (ب * ج)
القانون تبادلي
أ * ب = ب * أ
أ + ب = ب + أ
قانون التوزيع
أ * (ب + ج) = أ * ب + أ * ج
أ + (ب * ج) = أ + ب * أ + ج
قانون الهوية
أ * 0 = 0 أ *! = أ
أ +! =! أ + 0 = أ
قانون المجاملة
أ * ~ أ = 0
أ + ~ أ =!
قانون الالتفاف
~ (~ أ) = أ
قانون DeMorgan
~ (أ * ب) = ~ أ + ~ ب
~ (أ + ب) = ~ أ * ~ ب
كل قانون من القوانين المذكورة أعلاه موصوف في جزأين وهذا هو ثنائيات بعضهما البعض. مبدأ الازدواجية هو تبادل + (OR) & * (AND) عمليات ، 0 و 1 من التعبير.
من أجل فهم أفضل لمفهوم دائرة حاسبة الجبر المنطقية ، شرحنا هنا لتبسيط الجبر البولي. يتم شرح مثال تبسيط الجبر البولي أدناه.

مثال على تبسيط الجبر البوليني
تم تصميم الدائرة أعلاه مع بوابتين OR واثنين من بوابات NAND ، من الدائرة ، يمكننا الحصول على المعادلة مثل AB + BC (B + C) الموضحة في الشكل أعلاه. عندما يتم تطبيق قاعدة الهوية ونهائي العوامل على الدائرة المذكورة أعلاه ، فإن التعبير المبسط سيأخذ شكل بسيط.
وبالتالي ، هذا كل شيء عن الجبر البوليني دارة الآلة الحاسبة ، مخطط كتلة آلة حاسبة الجبر المنطقي ، مخطط دائرة حاسبة الجبر المنطقي ، تبسيط التعبير المنطقي ، قوانين الجبر المنطقية ومثال تبسيط الجبر البولي. نعتقد أن لديك فهمًا أفضل لهذا المفهوم ، علاوة على أي شكوك تتعلق بهذا الموضوع ، يرجى تقديم ملاحظاتك من خلال التعليق في قسم التعليقات أدناه ، إليك سؤال لك ، ما هي تطبيقات حاسبة الجبر المنطقية؟