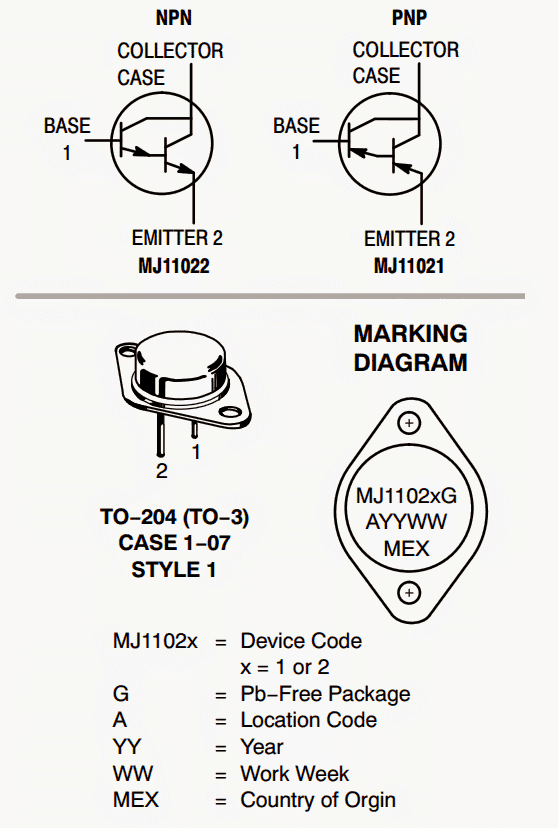
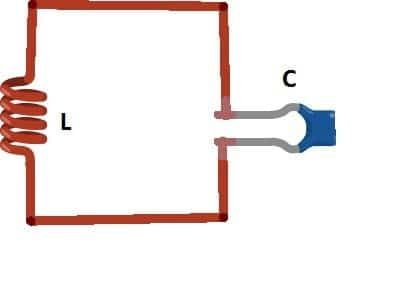
يمكن تخيل المحاثات على أنها عكس المكثفات. الفرق الرئيسي بين المكثف والمحث هو أن المكثف يحمل عازلًا واقيًا بين ألواحه ، مما يمنع توصيل التيار عبر أطرافه. هنا تعمل كدائرة مفتوحة.
من ناحية أخرى ، يكون الحث للمحث عادةً (وإن لم يكن دائمًا) منخفضًا بشكل لا يصدق أو أقل مقاومة. إنها تتصرف بشكل أساسي كدائرة مغلقة.
ازدواجية محث مكثف
يوجد مصطلح فريد في الإلكترونيات لهذا النوع من العلاقة بين معلمتين لدائرة أو أجزاء من الدائرة. تُعرف عناصر هذا النوع من الأزواج باسم ثنائيات من بعضها البعض . على سبيل المثال ، اعتمادًا على القدرة على إجراء التيار ، فإن الدائرة المفتوحة هي ثنائية الدائرة المغلقة.
وفقًا لنفس المبدأ ، يكون المحرِّض هو ثنائي المكثف. إن ازدواجية المحرِّضات والمكثفات أعمق بكثير من مجرد القدرة الطبيعية على توصيل التيار.
في هذه المقالة ، نقوم بمقارنة مبدأ العمل للمحث والمكثف وتقييم النتائج بالحسابات والصيغ.
على الرغم من أن لفائف عادة ونادرا ما ينظر في الدوائر الإلكترونية، منذ اليوم انها استبداله في الغالب من قبل opamps في lters فاي النشيطة)، والأجزاء الأخرى المعنية في الدائرة ويبدو أن تحمل بعض كمية من الحث.
يصبح الحث الذاتي لأطراف مكثف أو مقاوم مشكلة كبيرة في الدوائر عالية التردد ، وهو ما يفسر سبب استخدام المقاومات والمكثفات الخالية من الرصاص بشكل متكرر في مثل هذه التطبيقات.
معادلات المكثفات الأساسية
المعادلة الأساسية للمكثفات هي المعادلة التي يُعرف بها الفاراد:
C = Q / I [Eq.19]
حيث C هي السعة في فاراد ، Q هي الشحنة في كولوم ، و U هي pd بين الألواح بالفولت.
من خلال Eq. في الشكل 19 ، نحصل على صيغة بالصيغة Q = ∫ I dt + c حيث c هي الشحنة الأولية ، إذا كانت متاحة. بعد تحديد Q ، يمكننا تحديد U من Eq. 19:
U = 1 / C ∫ I dt + c / C. [مكافئ 21]
يمكن أن تكون إحدى الخصائص المهمة للمكثف مثل هذه ، إذا تم تطبيق تيار دوري عليه (عادةً تيار يتذبذب جيبيًا) ، فإن الشحنة على المكثف والجهد عبره يتقلبان أيضًا بشكل جيبي.
منحنى الشحنة أو الجهد هو منحنى جيب التمام السالب ، أو يمكننا تخيله على أنه منحنى جيبي يتخلف عن منحنى التيار بمقدار بي / 2 عملية (90 درجة).
المعادلة الأساسية التي تحدد هنري ، وحدة المحاثة ، هي
L = NΦ / أنا [مكافئ 22]
مع REFERNCE لفائف واحد، والحث الذاتي في هنري قد تكون العلاقة فلوريدا UX (المغناطيسي فلوريدا UX<1) in weber multiplied by the number of winding N, (because the magnetic flux cuts through each turn), when a unit current passes through it (I = 1 A). An even more handy definition could be extracted from Eq. 22, using Neumann’s equation. This claims that:
U = N (dΦ / dt) [مكافئ 23]
ما تقترحه هذه المعادلة هو حقيقة أن emf. الناجم داخل مغو نسبة إلى معدل مرتبطة تغير UX فل.
وأسرع في فلوريدا UX يختلف، وارتفاع e.m.f. التي يسببها على سبيل المثال ، عندما يرتفع التدفق فوق المحرِّض أو الملف بمعدل 2 ميغاواط ثانية-1، وبافتراض أن الملف يحتوي على خمسة وعشرين دورة ، فإن U = 25x2 = 50V.
طريق emf. هو من النوع الذي يقاوم الاختلافات في التدفق كما هو موضح في قانون لينز.
تتم الإشارة إلى هذه الحقيقة في كثير من الأحيان من خلال تسبق الجانب الأيمن من المعادلة بعلامة ناقص ، ولكن طالما أننا نعتقد أن U هي الجهة الخلفية ، فيمكن إزالة العلامة.
التفاضل
المصطلح dΦ / dt في Eq. 23 يشير إلى ما تعلمناه مثل معدل تغير UX فل. تسمى العبارة تفاضل Φ بالنسبة إلى t ، ويخصص فرع كامل من الحساب للعمل مع هذا النوع من التعبيرات. أخذت العبارة شكل رقم واحد (dΦ) مقسومًا على كمية أخرى (dt).
تُستخدم التفاضلات لربط مجموعات عديدة من النسب: dy / dx ، على سبيل المثال ، المتغيرات المترابطة x و y. عندما يتم رسم رسم بياني باستخدام قيم x عبر المحور الأفقي وقيم y عبر المحور الرأسي ، فإن dy / dx يشير إلى مدى انحدار الرسم البياني أو التدرج اللوني فيه.
إذا كان U هو جهد مصدر البوابة FET ، حيث T هو تيار التصريف المرتبط ، فإن dI / dU يشير إلى الكمية التي أتغير بها لتغييرات معينة في U. بدلاً من ذلك يمكننا القول ، dI / dU هو التوصيل التبادلي. في حين مناقشة المحاثات، يمكن أن يكون dΦ / دينارا معدل التغير في فلوريدا UX مع مرور الوقت.
يمكن اعتبار حساب التفاضل بمثابة إجراء معكوس للتكامل. لا توجد مساحة كافية في هذه المقالة للنظر في نظرية التفاضل ، ومع ذلك سنحدد جدول الكميات شائعة الاستخدام جنبًا إلى جنب مع فروقها.
التفاضلات القياسية

يعمل الجدول أعلاه باستخدام I و t كعاملين بدلاً من الروتين x و y. بحيث تكون تفاصيلها وثيقة الصلة بالإلكترونيات على وجه التحديد.
كمثال ، مع الأخذ في الاعتبار أن I = 3t +2 ، يمكن تصور الطريقة التي انحرف بها فيما يتعلق بالوقت في الرسم البياني للشكل 38. ولإيجاد معدل تغير I في أي لحظة ، فإننا نقدر dI / dt ، بواسطة في اشارة الى الجدول.

العنصر RST فاي في وظيفة غير 3T، أو لتنسيق بأنها فاي خط RST من الجدول، 3T1. إذا كان n = 1 ، يكون الفرق 3t1-1= 3 طن0.
منذ ر0= 1 ، الفرق هو 3.
الكمية الثانية هي 2 ، ويمكن التعبير عنها بـ 2t0.
يتغير هذا n = 0 ، وحجم التفاضل هو صفر. سيكون تفاضل الثابت صفرًا دائمًا. عند جمعهما معًا ، لدينا:
dI / dt = 3
في هذا الرسم التوضيحي ، لا يشمل التفاضل t ، وهذا يعني أن التفاضل لا يعتمد على الوقت.
وببساطة ، فإن ميل أو انحدار المنحنى في الشكل 38 هو 3 بشكل مستمر طوال الوقت. يوضح الشكل 39 أدناه منحنى دالة مختلفة ، I = 4 sin 1.5t.

بالإشارة إلى الجدول ، α = 1.5 و b = 0 في هذه الوظيفة. يوضح الجدول ، dl / dt = 4x1.5cos1.5t = 6cos 1.5t.
هذا يخبرنا بمعدل التغيير اللحظي I على سبيل المثال ، عند t = 0.4 ، dI / dt = 6cos0.6 = 4.95. يمكن ملاحظة ذلك في الشكل 39 ، حيث يتضمن منحنى 6 cos0.6t القيمة 4.95 عندما يكون t = 0.4.
يمكننا أيضًا ملاحظة أن ميل المنحنى 4sin1.5t يساوي 4.95 عندما يكون t = 0.4 ، كما يتضح من مماس المنحنى عند تلك النقطة (بالنسبة للمقاييس المختلفة على المحورين).
عندما تكون t = π / 3 ، نقطة يكون فيها التيار عند أعلى مستوياته وثابتًا ، في هذه الحالة dI / dt = 6cos (1.5xπ / 3): 0 ، وهو ما يعادل صفر تغير في التيار.
على العكس من ذلك ، عندما يكون t = 2π / 3 ويتحول التيار عند أعلى مستوى ممكن من الموجب إلى السالب ، dI / dt = 6cosπ = -6 ، نرى أعلى قيمة سلبية له ، مما يُظهر انخفاضًا كبيرًا في التيار.
الفائدة البسيطة من الفروق هي أنها تسمح لنا بتحديد معدلات التغيير للوظائف الأكثر تعقيدًا مقارنةً بـ I = 4sin 1.5t ، ودون الحاجة إلى رسم المنحنيات.
رجوع إلى العمليات الحسابية
من خلال إعادة تنظيم الشروط في Eq 22 نحصل على:
Φ = (L / N) أنا [مكافئ 24]
حيث L و N لهما أبعاد ثابتة ، لكن Φ وأنا قد يكون لهما قيمة فيما يتعلق بالوقت.
يعطي التفريق بين طرفي المعادلة فيما يتعلق بالوقت:
dΦ / dt = (L / N) (dI / dt) [مكافئ. 25]
يعطي دمج هذه المعادلة مع المعادلة 23:
U = N (L / N) (dI / dt) = L (dI / dt) [مكافئ 26]
هذه طريقة أخرى للتعبير عن هنري . يمكننا أن نقول ذلك ، ملف له تحريض ذاتي قدره 1 ساعة ، تغير في التيار بمقدار 1 أ ث-1يولد e.m.f. من 1 V. إعطاء وظيفة تحدد كيف يتغير التيار مع الوقت ، Eq. 26 يساعدنا على حساب الظهر e.m.f. مغو في أي لحظة.
فيما يلي بعض الأمثلة.
أ) أنا = 3 (تيار ثابت 3 أ) dl / dt = 0. لا يمكنك العثور على أي تغيير في التيار ، وبالتالي فإن e.m.f. هو صفر.
ب) أنا = 2t (تيار منحدر) dI / dt = 2 A s-1. مع ملف يحمل L = 0.25 H ، فإن ظهر e.m.f. سيكون ثابتًا عند 0.25 × 2 = 0.5 فولت.
C) I = 4sin1.5t (التيار الجيبي المعطى في الرسم التوضيحي السابق dl / dt = 6cos 1.5t. بالنظر إلى الملف مع L = 0.1 H ، فإن emf الخلفي اللحظي هو 0.6cos1.5t. يتبع emf الخلفي المنحنى التفاضلي من الشكل 39 ، ولكن بسعة 0.6 فولت بدلاً من 6 أ.
فهم 'الثنائيات'
تشير المعادلتان التاليتان إلى معادلة المكثف والمحث على التوالي:

يساعدنا في تحديد مستوى الجهد الناتج عبر المكون من خلال تغير التيار بمرور الوقت وفقًا لوظيفة معينة.
دعونا نقيم النتيجة التي حصلنا عليها التفريق الجانبين L و H من المعادلة 21 فيما يتعلق بالوقت.
dU / dt = (1 / C) أنا
بما أننا نعلم أن التفاضل هو معكوس التكامل ، فإن اشتقاق ∫I dt يعكس التكامل ، ونتيجة لذلك أنا فقط.
يعطي التفريق بين c / C صفرًا ، وإعادة ترتيب المصطلحات ينتج ما يلي:
أنا = C.dU / dt [مكافئ 27]
هذا يسمح لنا بمعرفة اتجاه التيار سواء كان يتجه نحو المكثف أو يخرج منه ، استجابة لجهد متغير وفقًا لوظيفة معينة.
الشيء المثير للاهتمام هو أن ما ورد أعلاه المعادلة الحالية للمكثف يبدو مشابهًا لمعادلة الجهد (26) لمحث ، والذي يعرض السعة ، ثنائية الحث.
وبالمثل ، يمكن أن يكون الفرق الحالي والجهد (pd) أو معدل تغير التيار و pd ثنائيًا عند تطبيقه على المكثفات والمحثات.
الآن ، دعنا ندمج المعادلة 26 فيما يتعلق بالوقت لإكمال المعادلة الرباعية:
∫ ش دت + ج = LI
تكامل dI / dt هو = I ، نعيد ترتيب التعبيرات للحصول على:
أنا = 1 / L∫ U dt + e / L.
يبدو هذا مرة أخرى مشابهًا تمامًا لـ Eq.21 ، مما يثبت الطبيعة المزدوجة للسعة والتحريض ، و pd والتيار.
لدينا الآن مجموعة من أربع معادلات يمكن استخدامها لحل المشكلات المتعلقة بالمكثف والمحث.
على سبيل المثال ، يمكن تطبيق Eq.27 لحل المشكلة مثل هذا:
مشكلة: تنتج نبضة الجهد المطبقة عبر 100 فائق التوهج منحنى كما هو موضح في الشكل أدناه.

يمكن تحديد ذلك باستخدام وظيفة القطعة التالية.

احسب التيار الذي يتحرك عبر المكثف وارسم الرسوم البيانية المقابلة.
المحلول:
بالنسبة للمرحلة الأولى نطبق المعادلة 27
أنا = C (dU / dt) = 0
للمثال الثاني حيث قد يرتفع U بمعدل ثابت:
I = C (dU / dt) = 3C = 300μA
هذا يدل على تيار شحن مستمر.
بالنسبة للمرحلة الثالثة عندما تسقط U بطريقة أسية:

يشير هذا إلى تدفق التيار بعيدًا عن المكثف بمعدل تناقص أسي.
علاقة المرحلة

في الشكل abobe ، يتم تطبيق pd بالتناوب على مغو. يمكن التعبير عن هذا pd في أي لحظة على النحو التالي:

حيث Uo هي ذروة قيمة pd. إذا قمنا بتحليل الدائرة في شكل حلقة ، وقمنا بتطبيق قانون جهد كيرشوف في اتجاه عقارب الساعة ، نحصل على:

ومع ذلك ، نظرًا لأن التيار جيبي هنا ، يجب أن يكون للمصطلحات الموجودة في القوس قيمة تساوي ذروة التيار Io ، لذلك نحصل أخيرًا على:

إذا قارنا المعادلة 29 ، والمكافئ 30 ، فسنجد أن التيار I والجهد U لهما نفس التردد ، وأنا متأخر عن U بمقدار π / 2.
يمكن دراسة المنحنيات الناتجة في الرسم البياني التالي:

ج
يوضح هذا العلاقة المتناقضة بين المكثف والمحث. بالنسبة لتيار المحرِّض ، يتأخر فرق الجهد بمقدار π / 2 ، بينما بالنسبة للمكثف ، يقود التيار pd. هذا يوضح مرة أخرى الطبيعة المزدوجة للمكونين.
زوج من: دائرة الإرسال 27 ميجا هرتز - نطاق 10 كيلومترات التالي: H-Bridge Bootstrapping