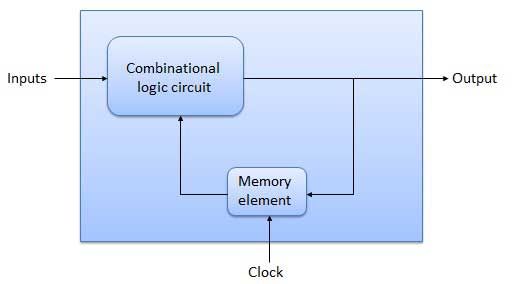
يتم إنشاء أنواع مختلفة من الأنظمة الرقمية من أنواع قليلة جدًا من تكوينات الشبكة الأساسية مثل بوابة AND ، بوابة NAND ، أو بوابة ، إلخ ... يتم استخدام هذه الدوائر الأولية مرارًا وتكرارًا في مجموعات طوبولوجية مختلفة. بالإضافة إلى أداء المنطق ، يجب على الأنظمة الرقمية أيضًا تخزين الأرقام الثنائية. لخلايا الذاكرة هذه ، والمعروفة أيضًا باسم نعال الشاطئ' ق مصممة. لأداء بعض الوظائف مثل الجمع الثنائي. وبالتالي ، لأداء مثل هذه الوظائف ، مجموعات من بوابات المنطق، بوابات منطقية و FLIP-FLOPs مصممة على شريحة IC أحادية الشريحة. تشكل هذه الدوائر المتكاملة اللبنات العملية للأنظمة الرقمية. أحد هذه اللبنات المستخدمة للإضافة الثنائية هو Carry Look-forward Adder.
ما هو Carry Look-forward Adder؟
يجب أن يحتوي الكمبيوتر الرقمي على دوائر يمكنها إجراء عمليات حسابية مثل الجمع والطرح والضرب والقسمة. من بين هذه العمليات ، الجمع والطرح هما العمليات الأساسية بينما الضرب والقسمة هما الجمع والطرح المتكرر على التوالي.
لتنفيذ هذه العمليات ، يتم تنفيذ 'دارات الأدير' باستخدام بوابات منطقية أساسية. دوائر الأفعى تم تطويرها كـ Half-adder و Full-adder و Ripple-Carry Adder و Carry Look-forward Adder.
من بين هؤلاء Carry Look-forward Adder هي دائرة الأفعى الأسرع. إنه يقلل من تأخير الانتشار ، الذي يحدث أثناء الإضافة ، باستخدام دوائر أجهزة أكثر تعقيدًا. تم تصميمه عن طريق تحويل دائرة أدير التموج بحيث يتم تغيير منطق حمل الأفعى إلى منطق من مستويين.
4-Bit Carry Look-forward Adder
في الإضافات المتوازية ، يتم إعطاء إخراج الحمل لكل أفعى كامل كمدخل حمل إلى الحالة التالية ذات الترتيب الأعلى. ومن ثم ، فإن هذه العناصر الإضافية لا يمكن إنتاج مخرجات حمل ومجموع لأي حالة ما لم يتوفر إدخال حمل لتلك الحالة.
لذلك ، لكي يحدث الحساب ، يجب على الدائرة الانتظار حتى تنتشر بتة الحمل في جميع الحالات. هذه المحفزات تحمل تأخير الانتشار في الدائرة.

4-بت-ريبل-كاري-أدير
ضع في اعتبارك دائرة تموج الحمل ذات 4 بت أعلاه. هنا يمكن إنتاج مجموع S3 بمجرد إعطاء المدخلات A3 و B3. ولكن لا يمكن حساب حمل C3 حتى يتم تطبيق بتة الحمل C2 بينما تعتمد C2 على C1. لذلك للحصول على نتائج الحالة المستقرة النهائية ، يجب أن ينتشر الحمل عبر جميع الولايات. هذا يزيد من تأخير انتشار الحمل للدائرة.
يتم حساب تأخير انتشار الأفعى على أنه 'تأخير انتشار كل بوابة مضروبًا في عدد المراحل في الدائرة'. لحساب عدد كبير من البتات ، يجب إضافة المزيد من المراحل ، مما يجعل التأخير أسوأ بكثير. ومن ثم ، لحل هذا الموقف ، تم تقديم Carry Look-forward Adder.
لفهم طريقة عمل Carry Look-forward Adder ، يتم وصف 4-bit Carry Look-forward Adder أدناه.

4-bit-Carry-Look-forward-Adder-Logic-Diagram
في هذا الأفعى ، يكون إدخال الحمل في أي مرحلة من مراحل الأفعى مستقلاً عن بتات الحمل التي تم إنشاؤها في المراحل المستقلة. هنا يعتمد إخراج أي مرحلة فقط على البتات التي تمت إضافتها في المراحل السابقة ومدخلات النقل المقدمة في مرحلة البداية. ومن ثم ، لا يتعين على الدائرة في أي مرحلة انتظار توليد بتة الحمل من المرحلة السابقة ويمكن تقييم بتة الحمل في أي لحظة زمنية.
جدول الحقيقة للحمل الأفعى
لاشتقاق جدول الحقيقة لهذا الأفعى ، تم تقديم مصطلحين جديدين - حمل التوليد وحمل الانتشار. حمل توليد Gi = 1 كلما تم إنشاء حمل Ci + 1. يعتمد ذلك على مدخلات Ai و Bi. تكون Gi 1 عندما تكون كل من Ai و Bi 1. وبالتالي ، يتم حساب Gi على أنها Gi = Ai. ثنائية.
يرتبط حمل النشر Pi بانتشار الحمل من Ci إلى Ci + 1. يتم حسابه على أنه Pi = Ai ⊕ Bi. يمكن اشتقاق جدول الحقيقة الخاص بهذا الأفعى من تعديل جدول الحقيقة الخاص بجماع كامل.
باستخدام مصطلحات Gi و Pi ، يتم إعطاء Sum Si و Carry Ci + 1 على النحو التالي -
- Si = Pi ⊕ Gi.
- Ci + 1 = Ci.Pi + Gi.
لذلك ، يمكن حساب بتات الحمل C1 و C2 و C3 و C4 على النحو التالي
- C1 = C0.P0 + G0.
- C2 = C1.P1 + G1 = (C0.P0 + G0) .P1 + G1.
- C3 = C2.P2 + G2 = (C1.P1 + G1) .P2 + G2.
- C4 = C3.P3 + G3 = C0.P0.P1.P2.P3 + P3.P2.P1.G0 + P3.P2.G1 + G2.P3 + G3.
يمكن ملاحظته من المعادلات التي تحمل Ci + 1 تعتمد فقط على C0 ، وليس على بتات الحمل الوسيطة.

حمل التطلع إلى الأمام الأفعى الحقيقة الجدول
مخطط الرسم البياني
يتم تنفيذ المعادلات أعلاه باستخدام الدوائر التوافقية ذات المستويين جنبًا إلى جنب مع بوابات AND و OR ، حيث يُفترض أن تحتوي البوابات على مدخلات متعددة.

حمل-إخراج-توليد-الدائرة-من-حمل-النظرة-الأفعى
ترد أدناه دائرة Carry Look-forward Adder لـ 4 بت.

4-bit-Carry-Look-forward-Adder-Circuit-الرسم التخطيطي
يمكن تصميم دوائر Carry Look-forward Adder ذات 8 بت و 16 بت من خلال تتابع دارة الأفعى المكونة من 4 بتات باستخدام منطق الحمل.
مزايا Carry Look-forward Adder
في هذا الأفعى ، يتم تقليل تأخير الانتشار. يعتمد إخراج الحمل في أي مرحلة فقط على بتة الحمل الأولية لمرحلة البداية. باستخدام هذا الأفعى ، من الممكن حساب النتائج الوسيطة. هذا الأفعى هو أسرع الأفعى المستخدمة في الحساب.
التطبيقات
يتم استخدام إضافات Carry Look-forward عالية السرعة كما تم تنفيذها مثل IC. وبالتالي ، من السهل تضمين الأفعى في الدوائر. من خلال الجمع بين اثنين أو أكثر من حسابات الجمع للوظائف المنطقية الأعلى يمكن القيام بها بسهولة. هنا تكون الزيادة في عدد البوابات أيضًا معتدلة عند استخدامها للبتات الأعلى.
بالنسبة لهذا الأفعى ، هناك مفاضلة بين المنطقة والسرعة. عند استخدامه لحسابات البتات الأعلى ، فإنه يوفر سرعة عالية ولكن تعقيد الدائرة يزداد أيضًا وبالتالي زيادة المساحة التي تشغلها الدائرة. عادةً ما يتم تنفيذ هذا الأفعى كوحدات 4 بت يتم تجميعها معًا عند استخدامها لإجراء حسابات أعلى. هذا الأفعى أغلى مقارنة بالآفات الأخرى.
بالنسبة للحساب المنطقي في أجهزة الكمبيوتر ، يتم استخدام الإضافات بانتظام. نفذ تشارلز باباج آلية لتوقع بتة الحمل في أجهزة الكمبيوتر لتقليل التأخير الذي تسببه تموج حمل الافعى . أثناء تصميم النظام ، تكون سرعة الحساب هي العامل الحاسم الأعلى للمصمم. في عام 1957 ، حصل Gerald B. Rosenberger على براءة اختراع لعقار Binary Carry Look-forward Adder الحديث. بناءً على تحليل تأخير البوابة والمحاكاة ، يتم إجراء تجارب لتعديل دائرة هذا الأفعى لجعله أسرع. بالنسبة إلى أفعى n-bit للحمل ، ما هو تأخير الانتشار ، عند إعطاء تأخير لكل بوابة هو 20؟
رصيد الصورة