في مجال الإلكترونيات ، تعتبر قاعدة مقسم الجهد بسيطة والأكثر أهمية دائرة كهربائية ، والذي يستخدم لتغيير جهد كبير إلى جهد صغير. باستخدام جهد i / p ومقاومات سلسلتين ، يمكننا الحصول على جهد o / p. هنا ، جهد الخرج هو جزء من جهد i / p. أفضل مثال على مقسم الجهد هو توصيل مقاومين في سلسلة. عندما يتم تطبيق جهد i / p عبر زوج المقاوم وسيظهر جهد o / p من الاتصال بينهما. بشكل عام ، تُستخدم هذه المقسمات لتقليل حجم الجهد أو لإنشاء جهد مرجعي ، كما تُستخدم عند الترددات المنخفضة كمخفف للإشارة. بالنسبة للتيار المستمر والترددات المنخفضة نسبيًا ، قد يكون مقسم الجهد مثاليًا بشكل مناسب إذا كان مصنوعًا فقط من مقاومات حيث تكون استجابة التردد مطلوبة على نطاق واسع.
ما هي قاعدة مقسم الجهد؟
تعريف: في مجال الإلكترونيات ، مقسم الجهد عبارة عن دائرة أساسية ، تُستخدم لتوليد جزء من جهد الدخل مثل الإخراج. يمكن تصميم هذه الدائرة بمقاومين أو أي مكونات سلبية مع مصدر جهد. يمكن توصيل المقاومات في الدائرة في سلسلة بينما يتم توصيل مصدر الجهد عبر هذه المقاومات. تسمى هذه الدائرة أيضًا بالمقسم المحتمل. يمكن أن ينتقل جهد الدخل بين المقاومين في الدائرة بحيث يحدث تقسيم الجهد.
متى تستخدم قاعدة مقسم الجهد؟
تُستخدم قاعدة مقسم الجهد لحل الدوائر لتبسيط الحل. يمكن أن يؤدي تطبيق هذه القاعدة أيضًا إلى حل الدوائر البسيطة تمامًا. المفهوم الرئيسي لقاعدة مقسم الجهد هذا هو 'يتم تقسيم الجهد بين مقاومين متصلين في سلسلة في تناسب مباشر مع مقاومتهما. يتضمن مقسم الجهد جزأين مهمين هما الدائرة والمعادلة.
مخططات تقسيم الجهد المختلفة
يتضمن مقسم الجهد مصدر جهد عبر سلسلة من مقاومين. قد ترى دوائر الجهد المختلفة مرسومة بطرق مختلفة موضحة أدناه. ولكن هذه دوائر مختلفة يجب أن تكون هي نفسها دائمًا.

مخططات تقسيم الجهد
في دوائر مقسم الجهد المختلفة أعلاه ، يكون المقاوم R1 هو الأقرب إلى جهد الدخل Vin ، والمقاوم R2 هو الأقرب إلى الطرف الأرضي. يسمى انخفاض الجهد عبر المقاوم R2 Vout وهو الجهد المقسم للدائرة.
حساب مقسم الجهد
دعونا نفكر في الدائرة التالية المتصلة باستخدام مقاومين R1 و R2. حيث يتم توصيل المقاوم المتغير بين مصدر الجهد. في الدائرة أدناه ، R1 هي المقاومة بين التلامس المنزلق للمتغير والطرف السالب. R2 هي المقاومة بين الطرف الموجب والاتصال المنزلق. هذا يعني أن المقاومتين R1 و R2 في سلسلة.

قاعدة مقسم الجهد باستخدام مقاومين
ينص قانون أوم على أن V = IR
من المعادلة أعلاه ، يمكننا الحصول على المعادلات التالية
V1 (t) = R1i (t) ........................... (I)
V2 (t) = R2i (t) ……………… (II)
تطبيق قانون الجهد كيرشوف
تنص KVL على أنه عندما يكون المجموع الجبري للجهد حول مسار مغلق في دائرة ما يساوي صفرًا.
-V (t) + v1 (t) + v2 (t) = 0
V (t) = V1 (t) + v2 (t)
وبالتالي
V (t) = R1i (t) + R2i (t) = i (t) (R1 + R2)
لذلك
i (t) = v (t) / R1 + R2 ………………. (ثالثا)
استبدال III في المعادلات الأولى والثانية
V1 (t) = R1 (v (t) / R1 + R2)
الخامس (ر) (R1 / R1 + R2)
V2 (t) = R2 (v (t) / R1 + R2)
الخامس (ر) (R2 / R1 + R2)
توضح الدائرة أعلاه مقسم الجهد بين المقاومين والذي يتناسب طرديا مع مقاومتهما. يمكن تمديد قاعدة مقسم الجهد إلى الدوائر المصممة بأكثر من مقاومين.

قاعدة مقسم الجهد باستخدام ثلاث مقاومات
حكم تقسيم الجهد لدارة المقاومتين أعلاه
V1 (t) = V (t) R1 / R1 + R2 + R3 + R4
V2 (t) = V (t) R2 / R1 + R2 + R3 + R4
V3 (t) = V (t) R3 / R1 + R2 + R3 + R4
V4 (t) = V (t) R4 / R1 + R2 + R3 + R4
معادلة مقسم الجهد
تقبل معادلة قاعدة مقسم الجهد عندما تعرف القيم الثلاث في الدائرة أعلاه ، فهي جهد الدخل وقيمتي المقاوم. باستخدام المعادلة التالية ، يمكننا إيجاد جهد الخرج.
قبو = فين. R2 / R1 + R2
تنص المعادلة أعلاه على أن Vout (جهد o / p) يتناسب طرديًا مع Vin (جهد الدخل) ونسبة اثنين من المقاومات R1 و R2.
مقسم جهد مقاوم
هذه دائرة سهلة وبسيطة للغاية للتصميم والفهم. يمكن بناء النوع الأساسي لدائرة مقسم الجهد السلبي بمقاومين متصلين في سلسلة. تستخدم هذه الدائرة قاعدة مقسم الجهد لقياس انخفاض الجهد عبر كل المقاوم المتسلسل. تظهر دائرة مقسم الجهد المقاوم أدناه.
في دائرة فاصل المقاومة ، يتم توصيل المقاومتين مثل R1 و R2 في سلسلة. لذا فإن تدفق التيار في هذه المقاومات سيكون هو نفسه. لذلك ، فإنه يوفر انخفاضًا في الجهد (I * R) عبر كل مقاومة.

نوع مقاوم
باستخدام مصدر الجهد ، يتم تطبيق مصدر جهد على هذه الدائرة. من خلال تطبيق قانون KVL & Ohms على هذه الدائرة ، يمكننا قياس انخفاض الجهد عبر المقاوم. لذلك يمكن إعطاء تدفق التيار في الدائرة على أنه
من خلال تطبيق KVL
VS = VR1 + VR2
وفقًا لقانون أوم
VR1 = I x R1
VR2 = I x R2
VS = I x R1 + I x R2 = I (R1 + R2)
أنا = VS / R1 + R2
تدفق التيار عبر الدائرة التسلسلية هو I = V / R وفقًا لقانون أوم. إذن تدفق التيار هو نفسه في كلا المقاومين. حتى الآن يمكن حساب انخفاض الجهد عبر المقاوم R2 في الدائرة
IR2 = VR2 / R2
مقابل / (R1 + R2)
VR2 = مقابل (R2 / R1 + R2)
وبالمثل ، يمكن حساب انخفاض الجهد عبر المقاوم R1 على النحو التالي
IR1 = VR1 / R1
مقابل / (R1 + R2)
VR1 = مقابل (R1 / R1 + R2)
مقسمات الجهد السعوي
تولد دائرة مقسم الجهد السعوي قطرات جهد عبر المكثفات المتصلة في سلسلة بمصدر تيار متردد. عادة ، يتم استخدام هذه لتقليل الفولتية العالية للغاية لتوفير إشارة جهد الخرج المنخفض. حاليًا ، هذه الفواصل قابلة للتطبيق في الأجهزة اللوحية والهواتف المحمولة وأجهزة العرض التي تعمل باللمس.
ليس مثل دوائر مقسم الجهد المقاوم ، تعمل مقسمات الجهد السعوية مع مصدر تيار متردد جيبي لأن تقسيم الجهد بين المكثفات يمكن حسابه بمساعدة مفاعلة المكثفات (Xج) يعتمد على تردد التيار المتردد.

نوع بالسعة
يمكن اشتقاق صيغة المفاعلة السعوية على شكل
Xc = 1 / 2πfc
أين:
Xc = مفاعلة سعوية (Ω)
π = 3142 (ثابت رقمي)
ƒ = التردد المُقاس بالهرتز (هرتز)
C = السعة المقاسة بالفاراد (F)
يمكن قياس مفاعلة كل مكثف بالجهد وتردد مصدر التيار المتردد واستبدالهما في المعادلة أعلاه للحصول على قطرات الجهد المكافئة عبر كل مكثف. دائرة مقسم الجهد السعوي موضحة أدناه.
باستخدام هذه المكثفات المتصلة في السلسلة ، يمكننا تحديد انخفاض الجهد RMS عبر كل مكثف من حيث مفاعلتها بمجرد توصيلها بمصدر جهد.
Xc1 = 1 / 2πfc1 & Xc2 = 1 / 2πfc2
XCT= سC1+ XC2
الخامسC1= مقابل (XC1/ XCT)
الخامسC2= مقابل (XC2/ XCT)
لا تسمح الفواصل السعوية بإدخال التيار المستمر.
المعادلة السعوية البسيطة لمدخل التيار المتردد هي
الخزنة = (C1 / C1 + C2)
مقسمات الجهد الاستقرائي
ستنشئ مقسمات الجهد الاستقرائي قطرات جهد عبر الملفات وإلا يتم توصيل المحاثات في سلسلة عبر مصدر تيار متردد. وهو يتألف من ملف لفائف مفردة يتم فصلها إلى جزأين أينما يتم استقبال جهد o / p من أحد الأجزاء.
أفضل مثال على مقسم الجهد الاستقرائي هذا هو المحول التلقائي بما في ذلك العديد من نقاط التنصت بملفه الثانوي. يمكن قياس مقسم الجهد الحثي بين اثنين من المحاثات من خلال مفاعلة المحرِّض المشار إليه بـ XL.

النوع الاستقرائي
يمكن اشتقاق صيغة المفاعلة الحثية
XL = 1 / 2πfL
'XL' هو تفاعل استقرائي يقاس بالأوم (Ω)
π = 3142 (ثابت رقمي)
'ƒ' هو التردد المُقاس بالهرتز (هرتز)
'L' هو محاثة تقاس في Henries (H)
يمكن حساب مفاعلة المحثين بمجرد أن نعرف التردد والجهد لمصدر التيار المتردد ونستخدمهما من خلال قانون مقسم الجهد للحصول على انخفاض الجهد عبر كل محث موضح أدناه. تظهر دائرة مقسم الجهد الاستقرائي أدناه.
باستخدام اثنين من المحرِّضين المتصلين في سلسلة في الدائرة ، يمكننا قياس انخفاض الجهد RMS عبر كل مكثف من حيث تفاعلهما بمجرد اتصالهما بمصدر جهد.
XL1= 2πfL1 & XL2= 2πfL2
XLT = XL1+ XL2
الخامسL1 = مقابل ( XL1/ XLT)
الخامسL2 = مقابل ( XL2/ XLT)
يمكن تقسيم مدخلات التيار المتردد بواسطة فواصل استقرائية بناءً على المحاثة:
صوت = (L2 / L1 + L2) * فين
هذه المعادلة مخصصة للمحثات التي لا تتفاعل وسيغير الحث المتبادل في المحول الذاتي النتائج. يمكن أن ينقسم مدخلات التيار المستمر بناءً على مقاومة العناصر وفقًا لقاعدة فاصل المقاومة.
مثال على مشاكل مقسم الجهد
يمكن حل مشاكل مثال مقسم الجهد باستخدام الدوائر المقاومة والسعوية والحثية المذكورة أعلاه.
1). لنفترض أن المقاومة الإجمالية للمقاوم المتغير هي 12 Ω. يتم وضع التلامس المنزلق عند النقطة التي تنقسم فيها المقاومة إلى 4 Ω و 8. يتم توصيل المقاوم المتغير عبر بطارية 2.5 فولت. دعونا نفحص الجهد الذي يظهر عبر الفولتميتر المتصل عبر المقطع 4 Ω من المقاوم المتغير.
وفقًا لقاعدة مقسم الجهد ، سيكون انخفاض الجهد ،
صوت = 2.5 فولت × 4 أوم / 12 أوم = 0.83 فولت
2). عندما يتم توصيل المكثفين C1-8uF و C2-20uF في سلسلة في الدائرة ، يمكن حساب قطرات الجهد RMS عبر كل مكثف عند توصيلهما بمصدر RMS 80 هرتز و 80 فولت.
Xc1 = 1 / 2cfc1
1/2 × 3.14 × 80 × 8 × 10-6 = 1 / 4019.2 × 10-6
= 248.8 أوم
Xc2 = 1/2 πfc2
1/2 × 3.14 × 80 × 20 × 10-6 = 1/10048 × 10-6
= 99.52 أوم
XCT = XC1 + XC2
= 248.8 + 99.52 = 348.32
VC1 = مقابل (XC1 / XCT)
80 (248.8 / 348.32) = 57.142
VC2 = مقابل (XC2 / XCT)
80 (99.52 / 348.32) = 22.85
3). عندما يتم توصيل المحاثين L1-8 mH و L2- 15 mH في سلسلة ، يمكننا حساب انخفاض الجهد RMS عبر كل مكثف بمجرد توصيلهما بـ 40 فولت ، 100 هرتز RMS.
XL1 = 2πfL1
= 2 × 3.14 × 100 × 8 × 10-3 = 5.024 أوم
XL2 = 2πfL2
= 2 × 3.14 × 100 × 15 × 10-3
9.42 أوم
XLT = XL1 + XL2
14.444 أوم
VL1 = مقابل (XL1 / XLT)
= 40 (5.024 / 14.444) = 13.91 فولت
VL2 = مقابل (XL2 / XLT)
= 40 (9.42 / 14.444) = 26.08 فولت
نقاط ضغط الجهد في شبكة مقسم
عندما يتم توصيل عدد المقاومات في سلسلة عبر مصدر جهد Vs في دائرة ، يمكن اعتبار نقاط التنصت على الجهد المختلفة على أنها A و B و C و D & E
يمكن حساب المقاومة الكلية في الدائرة بجمع جميع قيم المقاومة مثل 8 + 6 + 3 + 2 = 19 كيلو أوم. ستحد قيمة المقاومة هذه من تدفق التيار في جميع أنحاء الدائرة التي تولد مصدر الجهد (VS).
المعادلات المختلفة المستخدمة لحساب انخفاض الجهد عبر المقاومات هي VR1 = VAB ،
VR2 = VBC و VR3 = VCD و VR4 = VDE.
يتم حساب مستويات الجهد عند كل نقطة نقر فيما يتعلق بمحطة GND (0V). لذلك ، فإن مستوى الجهد عند النقطة 'D' سيكون مكافئًا لـ VDE ، بينما مستوى الجهد عند النقطة 'C' سيكون مكافئًا لـ VCD + VDE. هنا ، مستوى الجهد عند النقطة 'C' هو مقدار انخفاض الجهد عبر مقاومين R3 و R4.
لذلك من خلال اختيار مجموعة مناسبة من قيم المقاوم ، يمكننا إجراء سلسلة من انخفاضات الجهد. سيكون لهذا الانخفاض في الجهد قيمة جهد نسبي يتم الحصول عليها من الجهد فقط. في المثال أعلاه ، تكون كل قيمة جهد o / p موجبة حيث يتم توصيل الطرف السالب لمصدر الجهد (VS) بالطرف الأرضي.
تطبيقات مقسم الجهد
ال تطبيقات مقسم الاقتراع تشمل ما يلي.
- يتم استخدام مقسم الجهد فقط حيث يتم تنظيم الجهد عن طريق إسقاط جهد معين في الدائرة. تستخدم بشكل أساسي في مثل هذه الأنظمة حيث لا يتم بالضرورة اعتبار كفاءة الطاقة على محمل الجد.
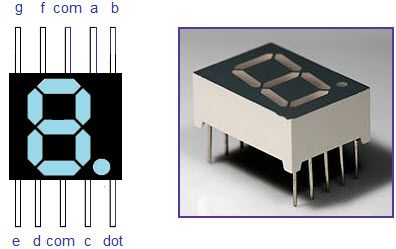
- في حياتنا اليومية ، يتم استخدام مقسم الجهد في مقاييس فرق الجهد. أفضل الأمثلة لمقاييس الجهد هي مقبض ضبط مستوى الصوت المرفق بأنظمتنا الموسيقية وترانزستورات الراديو ، إلخ. يشتمل التصميم الأساسي لمقياس الجهد على ثلاثة دبابيس موضحة أعلاه. في ذلك ، يتم توصيل دبابيس بالمقاوم الموجود داخل مقياس الجهد ويتم توصيل الدبوس المتبقي بملامس مسح ينزلق على المقاوم. عندما يغير شخص ما المقبض الموجود على مقياس الجهد ، سيظهر الجهد عبر جهات الاتصال المستقرة ويمسح جهة الاتصال وفقًا لقاعدة مقسم الجهد.
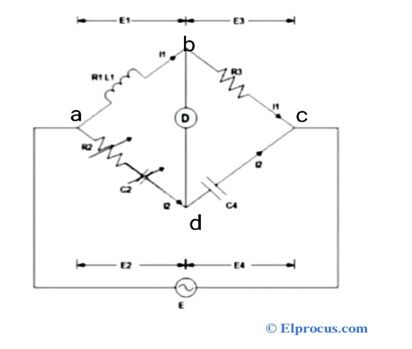
- تستخدم مقسمات الجهد لضبط مستوى الإشارة ، لقياس الجهد وانحياز الأجهزة النشطة في مكبرات الصوت. يتضمن جسر متعدد المقاييس وجسر ويتستون فواصل الجهد.
- يمكن استخدام فواصل الجهد لقياس مقاومة المستشعر. لتشكيل مقسم جهد ، يتم توصيل المستشعر في سلسلة بمقاومة معروفة ، ويتم تطبيق الجهد المعروف عبر الحاجز. ال محول تناظري رقمي المتحكم الدقيق متصل بالصنبور المركزي للمقسم بحيث يمكن قياس جهد الضغط. باستخدام المقاومة المعروفة ، يمكن حساب مقاومة مستشعر الجهد المقاس.
- تستخدم مقسمات الجهد في قياس المستشعر ، والجهد ، وتحول المستوى المنطقي ، وضبط مستوى الإشارة.
- بشكل عام ، تُستخدم قاعدة مقسم المقاوم بشكل أساسي لإنتاج الفولتية المرجعية أو تقليل حجم الجهد بحيث يكون القياس بسيطًا جدًا. بالإضافة إلى ذلك ، تعمل هذه الأجهزة كمخفف للإشارة بتردد منخفض
- يتم استخدامه في حالة وجود ترددات أقل للغاية و DC
- مقسم الجهد السعوي المستخدم في نقل الطاقة لتعويض سعة الحمل وقياس الجهد العالي.
هذا كل شيء حول تقسيم الجهد مع الدوائر ، تنطبق هذه القاعدة على مصادر جهد التيار المتردد والتيار المستمر. علاوة على ذلك ، فإن أي شكوك بخصوص هذا المفهوم أو مشاريع الإلكترونيات والكهرباء ، يرجى إبداء ملاحظاتك عن طريق التعليق في قسم التعليقات أدناه. إليك سؤال لك ، ما هي الوظيفة الأساسية لقاعدة مقسم الجهد؟